Il Teorema di Bayes Un Approccio Probabilistico

Introduzione al Teorema di Bayes: Bayesian

Immaginate di essere un medico e di dover diagnosticare una malattia. Avete un paziente con alcuni sintomi specifici e volete capire la probabilità che abbia una particolare condizione. In questo caso, il Teorema di Bayes può essere un potente strumento per aiutarvi a prendere una decisione informata.

Il Teorema di Bayes è una formula matematica che ci permette di aggiornare la nostra conoscenza di un evento sulla base di nuove informazioni. In altre parole, ci aiuta a capire come la probabilità di un evento cambia quando abbiamo nuove prove a disposizione.

Applicazioni del Teorema di Bayes

Il Teorema di Bayes ha un’ampia gamma di applicazioni in diversi campi, tra cui:

• Medicina: Come già detto, il Teorema di Bayes è utilizzato per diagnosticare malattie. I medici possono utilizzare la formula per calcolare la probabilità che un paziente abbia una certa malattia, date le sue caratteristiche cliniche.
• Finanza: Gli analisti finanziari utilizzano il Teorema di Bayes per valutare il rischio e la redditività degli investimenti. Possono ad esempio utilizzare la formula per calcolare la probabilità che un’azienda fallisca, tenendo conto dei suoi dati finanziari.
• Intelligenza Artificiale: Il Teorema di Bayes è alla base di molti algoritmi di apprendimento automatico, come i filtri antispam e i sistemi di riconoscimento facciale. Questi algoritmi utilizzano la formula per imparare dai dati e migliorare le loro prestazioni nel tempo.

Confronto con altri metodi di inferenza statistica

Il Teorema di Bayes è un metodo di inferenza statistica, che significa che ci permette di trarre conclusioni da dati. Esistono altri metodi di inferenza statistica, come il metodo frequentista.

La principale differenza tra il Teorema di Bayes e il metodo frequentista è che il primo è basato sulla probabilità soggettiva, mentre il secondo è basato sulla probabilità oggettiva. La probabilità soggettiva è la nostra credenza sulla probabilità di un evento, mentre la probabilità oggettiva è la frequenza relativa con cui un evento si verifica.

Il Teorema di Bayes è particolarmente utile quando abbiamo informazioni a priori, ovvero informazioni che abbiamo prima di osservare i dati. Ad esempio, se sappiamo che una certa malattia è rara, possiamo usare questa informazione a priori per aggiornare la nostra credenza sulla probabilità che un paziente abbia quella malattia, dato che presenta alcuni sintomi.

Il Teorema di Bayes è una formula matematica che ci permette di aggiornare la nostra conoscenza di un evento sulla base di nuove informazioni.

Applicazioni del Teorema di Bayes

Il Teorema di Bayes è un potente strumento che ci permette di aggiornare le nostre credenze sulla base di nuove informazioni. In sostanza, ci dice come la probabilità di un evento cambia quando abbiamo nuove informazioni. È un principio fondamentale che trova applicazione in molti campi, dalla medicina alla finanza, dalla scienza forense all’intelligenza artificiale.

Esempi di Applicazione del Teorema di Bayes

Vediamo alcuni esempi concreti di come il Teorema di Bayes viene utilizzato in diversi settori.

Medicina

Il Teorema di Bayes viene utilizzato in medicina per calcolare la probabilità che un paziente abbia una particolare malattia, dato che ha presentato determinati sintomi. Ad esempio, un medico potrebbe usare il Teorema di Bayes per calcolare la probabilità che un paziente abbia il cancro al seno, dato che ha un nodulo al seno. Il medico potrebbe considerare la probabilità a priori del cancro al seno nella popolazione generale, la sensibilità del test per il cancro al seno e la specificità del test.

Finanza

In finanza, il Teorema di Bayes può essere utilizzato per calcolare la probabilità che un’azienda fallisca, dato che ha presentato determinate performance finanziarie. Ad esempio, un analista finanziario potrebbe usare il Teorema di Bayes per calcolare la probabilità che un’azienda fallisca, dato che ha un alto rapporto debito/patrimonio netto. L’analista potrebbe considerare la probabilità a priori di fallimento per le aziende con un alto rapporto debito/patrimonio netto, la sensibilità di questo rapporto nel predire il fallimento e la specificità di questo rapporto nel predire il fallimento.

Scienza Forense

Il Teorema di Bayes viene utilizzato in scienza forense per calcolare la probabilità che un sospettato sia colpevole, dato che è stato trovato sul luogo del delitto. Ad esempio, un perito forense potrebbe usare il Teorema di Bayes per calcolare la probabilità che un sospettato sia colpevole, dato che le sue impronte digitali sono state trovate sulla scena del crimine. Il perito potrebbe considerare la probabilità a priori che un sospettato sia colpevole, la probabilità che le sue impronte digitali siano state trovate sulla scena del crimine se fosse colpevole e la probabilità che le sue impronte digitali siano state trovate sulla scena del crimine se fosse innocente.

Intelligenza Artificiale

Il Teorema di Bayes è alla base di molti algoritmi di intelligenza artificiale, come i filtri antispam e i sistemi di riconoscimento facciale. Ad esempio, un filtro antispam potrebbe usare il Teorema di Bayes per calcolare la probabilità che un’email sia spam, dato che contiene determinate parole chiave. Il filtro potrebbe considerare la probabilità a priori che un’email sia spam, la probabilità che un’email contenga determinate parole chiave se è spam e la probabilità che un’email contenga determinate parole chiave se non è spam.

Aggiornamento delle Credenze

Il Teorema di Bayes è uno strumento potente per aggiornare le nostre credenze alla luce di nuove informazioni. In sostanza, ci dice come la probabilità di un evento cambia quando abbiamo nuove informazioni. Ad esempio, se abbiamo una credenza a priori sulla probabilità che un evento si verifichi, e poi riceviamo nuove informazioni, possiamo usare il Teorema di Bayes per aggiornare la nostra credenza.

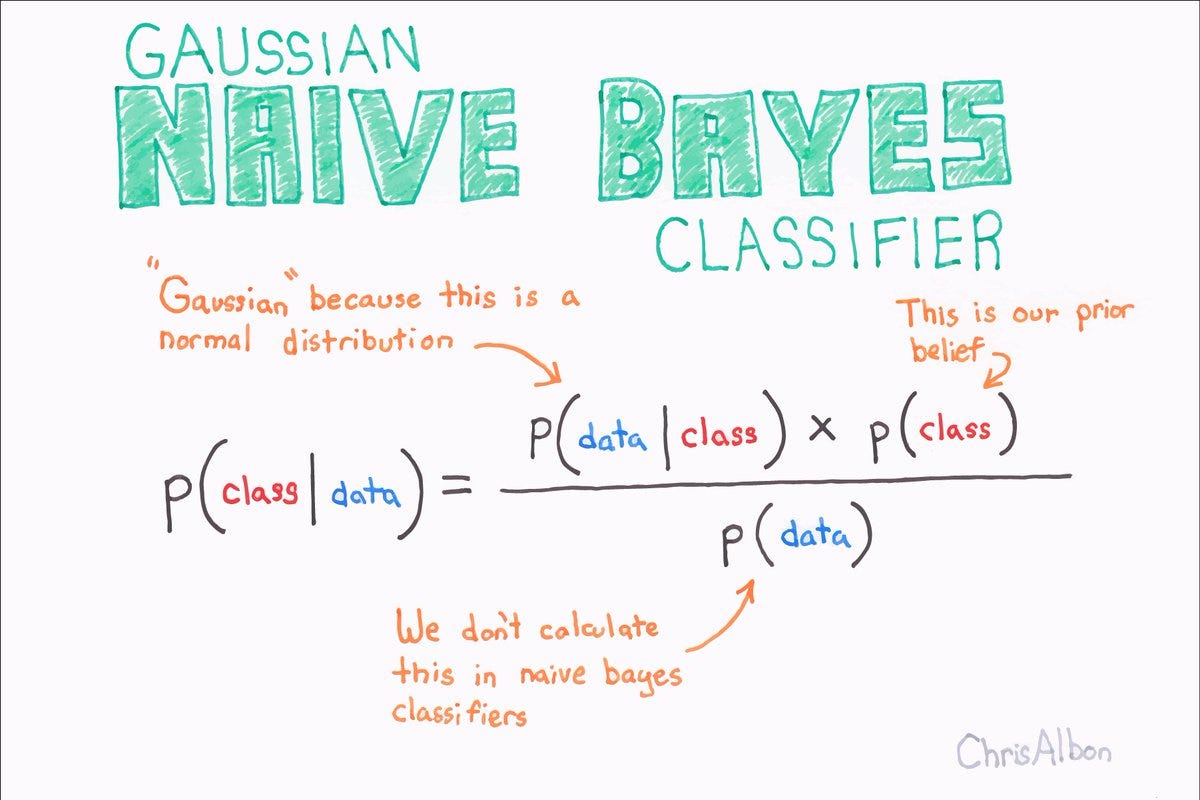
La formula del Teorema di Bayes è la seguente:

P(A|B) = [P(B|A) * P(A)] / P(B)

dove:

* P(A|B) è la probabilità di A dato B.
* P(B|A) è la probabilità di B dato A.
* P(A) è la probabilità a priori di A.
* P(B) è la probabilità a priori di B.

Il Teorema di Bayes ci permette di aggiornare le nostre credenze in modo razionale e sistematico. È uno strumento fondamentale per prendere decisioni in situazioni di incertezza.

Approfondimenti sul Teorema di Bayes

Abbiamo visto come il Teorema di Bayes può essere applicato per aggiornare la nostra conoscenza di un evento, dato un nuovo dato. Ora, andiamo a esplorare alcuni aspetti più profondi del teorema, che ci permetteranno di comprenderlo in modo più completo.

Interpretazioni del Teorema di Bayes, Bayesian

Il Teorema di Bayes può essere interpretato in due modi principali: la visione frequentista e la visione bayesiana. La visione frequentista considera la probabilità come la frequenza relativa di un evento in un numero infinito di prove. In questo contesto, la probabilità di un evento è definita come il limite della frequenza relativa dell’evento quando il numero di prove tende all’infinito. La visione bayesiana, invece, considera la probabilità come una misura del grado di fiducia in un evento, basata sulle informazioni disponibili. In questo contesto, la probabilità di un evento può essere aggiornata man mano che si acquisiscono nuove informazioni.

• La visione frequentista è basata sull’idea che la probabilità di un evento possa essere determinata osservando la frequenza relativa dell’evento in un numero infinito di prove. Ad esempio, se lanciamo una moneta 100 volte e otteniamo 50 teste, la probabilità di ottenere testa è 0,5. Questa interpretazione è spesso utilizzata in contesti scientifici e ingegneristici, dove è possibile effettuare un numero elevato di prove.
• La visione bayesiana, invece, considera la probabilità come una misura del grado di fiducia in un evento, basata sulle informazioni disponibili. Ad esempio, se sappiamo che il 10% della popolazione soffre di una certa malattia, possiamo assegnare una probabilità del 10% al fatto che una persona scelta a caso soffra di quella malattia. Se poi otteniamo nuove informazioni, come il fatto che la persona in questione presenta alcuni sintomi specifici, possiamo aggiornare la probabilità della malattia. Questa interpretazione è spesso utilizzata in contesti decisionali, dove è necessario prendere decisioni in base alle informazioni disponibili.

Utilizzo del Teorema di Bayes nell’Apprendimento Automatico

Il Teorema di Bayes è un elemento fondamentale nell’apprendimento automatico, in particolare nei modelli di classificazione. In questi modelli, l’obiettivo è classificare nuovi dati in base a un insieme di dati di addestramento. Il Teorema di Bayes può essere utilizzato per calcolare la probabilità che un nuovo dato appartenga a una certa classe, data la sua distribuzione di probabilità condizionata rispetto alle diverse classi.

• Ad esempio, in un modello di classificazione di spam, il Teorema di Bayes può essere utilizzato per calcolare la probabilità che un’email sia spam, dato il suo contenuto. Il modello di classificazione può quindi utilizzare questa probabilità per decidere se contrassegnare l’email come spam o meno.

Limiti e Sfide nell’Applicazione del Teorema di Bayes

Sebbene il Teorema di Bayes sia uno strumento potente, è importante essere consapevoli dei suoi limiti e delle sfide nell’applicazione.

• Uno dei limiti principali è la necessità di avere una conoscenza preliminare della distribuzione di probabilità delle diverse classi. In alcuni casi, questa conoscenza può essere difficile da ottenere o può essere imprecisa. Questo può portare a risultati imprecisi o a una cattiva classificazione dei dati.
• Un’altra sfida è la complessità computazionale del calcolo della probabilità a posteriori, soprattutto quando si hanno molte classi o molti attributi. In questi casi, possono essere necessari algoritmi di approssimazione per rendere il calcolo più efficiente.
• Inoltre, il Teorema di Bayes può essere sensibile alla presenza di dati anomali, che possono influenzare la distribuzione di probabilità delle diverse classi. È quindi importante utilizzare tecniche di pre-elaborazione dei dati per identificare e gestire i dati anomali.

Bayesian statistics, it’s like, the hot new thing in data analysis, right? It’s all about updating your beliefs based on new evidence, kind of like how you might change your mind about a new band after listening to their latest album.

But it’s not just for music nerds, it’s used in everything from medical research to financial modeling. Even Mike Lynch, the UK entrepreneur who’s been in the news lately, mike lynch uk , is using Bayesian methods to make decisions.

So, yeah, Bayesian stuff is pretty cool, even if it sounds a little complicated.

Bayesian statistics, man, it’s all about making smart decisions based on the data you have. Think of it like a savvy tycoon, using every bit of information to make the best move. Like the tycoon in that article, you’ve gotta be able to weigh the odds and calculate your next step.

That’s the essence of Bayesian thinking – using probabilities to guide your decisions and maximize your chances of success.